Juan-Carlos Toledo-Salas, Ph.D.
My oil paintings
Here are my oil paintings.
 Grullas, May 2021 |  Present, past and future. March2020 |  Orange still life, Augost 2020 |
|---|---|---|
 DNA polimerase I, May 2019 |  Still life, March 2019 |  Still life, Dec 2018 |
 LIbrary "Mario de Andrade" |  Still life, Nov 2018 |  Life doors, Sept 2018 |
 Breakfast, Aug 2018 |  Yamanaka, 山中, Jun 2018 |  Enzyme May 2018 |
 Winter Jan 2018 |  Brain Dec 2017 |  Sesc Oct 2017 |
 Kinkakuji 金閣寺 Oct 2017 |  Train Sep 2017 |  Cubism of Igreja do Carmo, Aug 2017 |
 Cubism, Aug 2016 |  Everick Ayala M.D.Radiology, Nov2016 |  Surrealism, Oct 2016 |
 Electrophysiological recordings. |  Time and gravity, 2014. |  Marta Hiroko Kato |
 Still life, 2013 |  Igreja do Carmo, Jul 2016 |  American Church, Jun 2016 |
 Cylinders, Nov 2015 |  Still life, Jan 2016 |  Still life, Nov 2015 |
 Japanese woman. |  Marta Hiroko Kato, Oct 2015 |  Dr.Peever laboratory, Jan 2012 |
 Still life, Oct 2015 |  Igreja Santa Cruz, Jul 2016 |
Mathematical figures
When exploring nature, we see that there are many symmetric structures (like the roots of plants, starfishes, shells, etc.) and that symmetry seems to be conserved and expressed in different beings. The shape and symmetry of most of those structures are defined by homoetic genes which have been conserved and transmitted by inheritance, and how the gene products influence and shapes the structure development is defined by their diffusion rate within that structure. Considering that during diffusion the concentration diminishes from their origin (where concentration is maximum) with time, drawings can be made following that pattern, imitate nature or create new patterns.
Here there is the shell of a snail I made just by using symmetric shapes of different sizes colliding and joining points and edges using curves.
The image started from an hexagon (light blue lines) and several (six) hexagons of smaller size were drawn inside the largest one. The largest hexagon was joined to the next largest and so one (in anticlockwise pattern). The external angle of one hexagon joined the internal angle of the consecutive hexagon, and its internal angle was joined to the external angle of the next hexagon and so on, moving anticlockwise. Then curves were drawn from the hexagon points to the angles of the smallest hexagon following an anticlockwise pattern.

The symmetric figures can also follow the famous Fibonacci sequence: increasing by adding the previous value to the next one:
0,1,1,2,3,5,8,13,21,34...
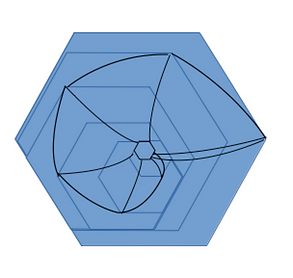
The left picture shows four rectangles, each one following that sequence. It can be changed to give a three-dimensional figure using oblique lines joining corners to a central point.
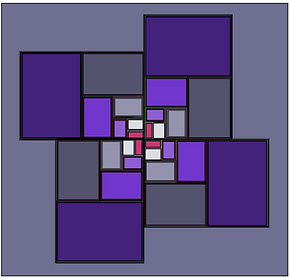
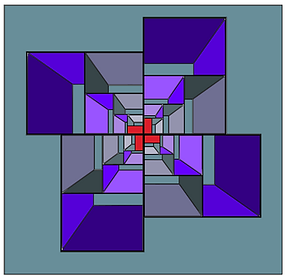
By joining many of the left figure together by the borders another more complex and amazing figure can be made. New blank rectangle gaps appear, and a nice art combination is made, as below:

There are many mathematical problems considering symmetry that are hard to solve. One of the most famous is the Basel problem which was solved by Euler. This problem was :
1+1/4+1/9+1/16+1/25+1/16+....
The solution is : π *π/6 .
Here the famous π number related to circles properties appears.
Another very interesting image is the Reuleaux triangle. It is a curved triangle which is inside a square but always touching its always the four square borders, no matter how it rotates. Its movie is shown in the left side.
There are structures called Cardioid. They have similar shape as biological structures like a kidney, beans, etc. They are made by joining points in the circumference of a circle. In Cardioid x2, each point will join its double (1 joins 2, 2 joins 4, 3 joins 6, etc) and Cardioid x3, Cardioid x4, etc can made. As more points in the circumference are drawn, a better resolution is obtained.
That figure is also obtained when rotating a circle through the circumference of another circle. When changing the proportions of radius of the rotating circle to the radius more complex Cardiods can be obtained.

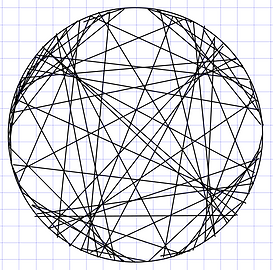
Other nice pictures can be made when using a square instead of a circle, and joining the points of continuous perimeters.
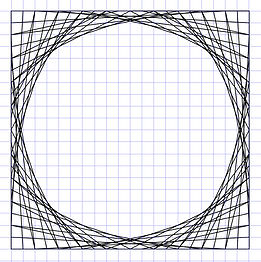
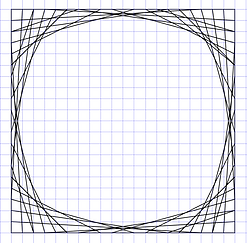
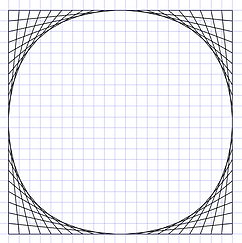
When joining continuous perimeters in opposite directions different figures are made.
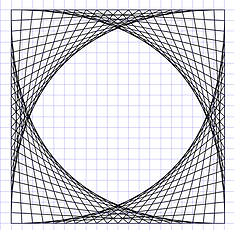
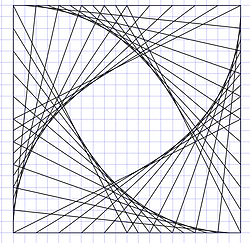
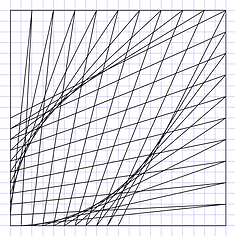
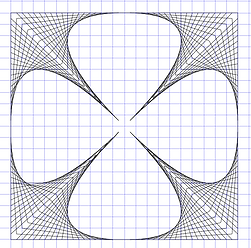

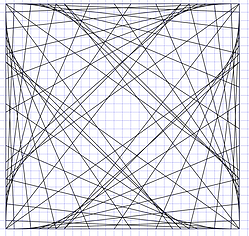
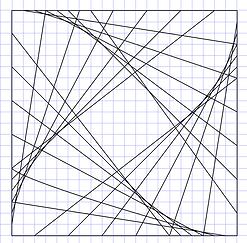
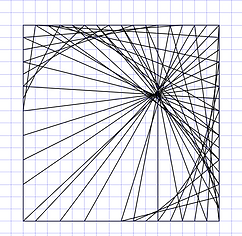
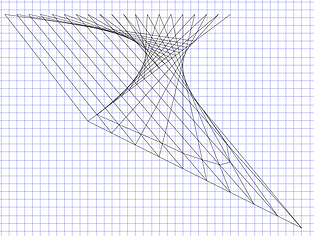
Similar pictures can also be using in octagons, circles or even just straight lines. We see curves but light travels in straight lines (except when affected by huge forces of gravity). Our nervous system should analyze all those straight patterns of light to let us see spheroids.



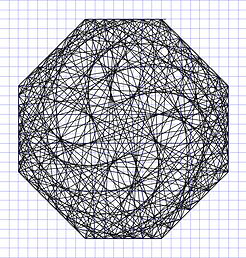
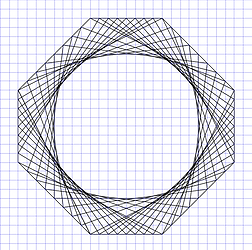

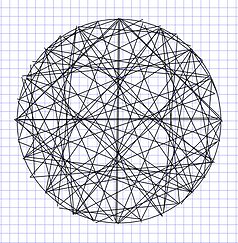


These figures can also be painted, I used Inskscape to draw them. Inkscape is free, not expensive like Adobe and Corel Draw. Here are some pictures I painted.

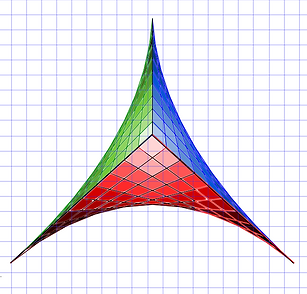
Making graphs can also be related to mathematics. After watching some videos of Mathloger, there was something very interesting. This numerical sequence was shown: 1,2,4,8,16... and they asked which is the next number ...Most of us will say its 32...but that is not always right. More information is needed. In this case it refers to the number of spaces in a circle after lines joining points in the circumference are drawn, spaces in circle after 1,2,3,4,5... points joined in the circumference in this way (points in black, spaces in red):